Hledej
Zobraz:
Univerzity
Kategorie
Rozšířené vyhledávání
12 662
projektů
Reálná funkce dvou a více proměnných - I
| Přípona |
Typ studijní materiál |
Stažené 52 x |
| Velikost 0,8 MB |
Jazyk český |
ID projektu 2310 |
| Poslední úprava 06.11.2013 |
Zobrazeno 2 472 x |
Autor: jullie.kanska |
 Sdílej na Facebooku
Sdílej na Facebooku |
||
| Detaily projektu | ||
- Cena:
0 Kreditů - kvalita:
93,2% -
Stáhni
- Přidej na srovnání
- Univerzita:Vysoké učení technické v Brně
- Fakulta:Fakulta stavební
- Kategorie:Přírodní vědy » Matematika
- Předmět:Matematika
- Studijní obor:-
- Ročník:1. ročník
- Formát:PDF dokument (.pdf)
- Rozsah A4:50 stran
Při studiu funkčních závislostí různých veličin v matematice, fyzice i technických předmětech, nevystačíme s reálnou funkcí jedné reálné proměnné a používáme proto funkce dvou, tří, nebo více proměnných. Uveďme si některé konkrétní příklady takových funkcí.
Klíčová slova:
Funkce dvou proměnných
složená funkce
limita
spojitost
parciální derivace
totální diferenciál
Taylorova věta
Obsah:
- Úvod
Cíle
Požadované znalosti
Doba potřebná ke studiu
Klíčová slova
Metodický návod k práci s textem
Funkce dvou a více proměnných
Pojem funkce dvou a více proměnných
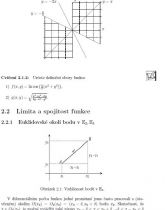
Limita a spojitost funkce
Euklidovské okolí bodu v E2, E3
Některé množiny E2
Limita posloupností
Limita funkce
Spojitost funkce
Parciální derivace
Parciální derivace funkce dvou proměnných
Parciální derivace funkce více proměnných
Vztah mezi existencí parciálních derivací a spojitostí funkce
Parciální derivace vyšších řádů
Složená funkce
Složená funkce dvou a více proměnných
Parciální derivace složené funkce
Totální diferenciál funkce
Pjem totálního diferenciálu
Totální difereciály vyšších řádů
Taylorova věta
Zdroje:
- Anton H., Calculus with Analytic Geometry, John Wiley, 1995.
- Brabec J., Hrùza B., Matematická analýza II, SNTL, Praha 1986.
- Èermáková H. a kolektiv, Sbírka pøíkladù z matematiky II, VUT, FAST,
- CERM, Brno 2003.
- Do¹lá Z., Do¹lý O., Diferenciální poèet funkcí více promìnných, Masarykova
- univerzita, Pøírodovìdecká fakulta, Brno 1999.
- Drábek P., Míka S., Matematická analýza II, Západoèeská univerzita v Plzni,
- Fakulta aplikovaných vìd, Plzeò 1999.
- Elia¹ J., Horváth J., Kajan J. Zbierka úloh z vy¹¹ej matematiky, 3. èas», Alfa,
- Bratislava 1971 (2. vydanie).
- Ivan J., Matematika II, Alfa, Bratislava 1989.
- Karásek J., Matematika II, VUT, FSI, CERM, Brno 2002.
- Kluvánek J., Mi¹ík L., ©vec M., Matematika I, SVTL, Bratislava 1959