Hledej
Zobraz:
Univerzity
Kategorie
Rozšířené vyhledávání
12 662
projektů
Vypracované otázky z předmětu Betónové a zděné konstrukce
| Přípona .docx |
Typ vypracované otázky |
Stažené 51 x |
| Velikost 8,1 MB |
Jazyk český |
ID projektu 6409 |
| Poslední úprava 10.08.2015 |
Zobrazeno 7 799 x |
Autor: jiri.hosko |
 Sdílej na Facebooku
Sdílej na Facebooku |
||
| Detaily projektu | ||
- Cena:
4 Kreditů - kvalita:
92,3% -
Stáhni
- Přidej na srovnání
- Univerzita:Vysoká škola technická a ekonomická v Českých Budějovicích
- Fakulta:-
- Kategorie:Technika » Stavebnictví
- Předmět:Betonové a zděné konstrukce
- Studijní obor:-
- Ročník:3. ročník
- Formát:MS Office Word (.docx)
- Rozsah A4:37 stran
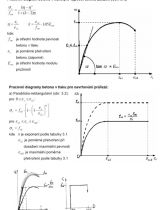
1. Pracovní diagram betonu
{diagramy}
2. Pracovní diagram oceli
1.) Mez úměrnosti (U)
Závislost mezi napětím a přetvořením je až do meze úměrnosti vyjádřena Hookovým zákonem
σ = ε . E
Kde E je modul pružnosti oceli a ε je poměrné prodloužení. Ocel se chová jako dokonale pružný materiál.
E = 2,1 • 105 MPa
2.) Mez pružnosti (E)
Do dosažení této meze se ocel ještě chová jako pružný materiál. ε = 0,05%
3.) Mez kluzu (K)
Při dosažení meze kluzu se porušuje soudržnost mezi ocelí a betonem. Po dosažení meze kluzu se ocel stává plastickou. Deformace se zvětšuje aniž by rostlo napětí. U ocelí s nevýraznou mezí kluzu, bereme napětí, při kterém je hodnota přetvoření 0,2%.
4.) Mez pevnosti (P)
Po dosažení meze pevnosti se přetvoření prutu dále zvětšuje, i když napětí v prutu klesá. Přetvoření se zvětšuje až do meze destrukce.
5.) Mez destrukce (D)
Při dosažení této meze se prut přetrhne, poměrné přetvoření v okamžiku destrukce je tažnost oceli (okolo 14%).
{diagramy}
2. Pracovní diagram oceli
1.) Mez úměrnosti (U)
Závislost mezi napětím a přetvořením je až do meze úměrnosti vyjádřena Hookovým zákonem
σ = ε . E
Kde E je modul pružnosti oceli a ε je poměrné prodloužení. Ocel se chová jako dokonale pružný materiál.
E = 2,1 • 105 MPa
2.) Mez pružnosti (E)
Do dosažení této meze se ocel ještě chová jako pružný materiál. ε = 0,05%
3.) Mez kluzu (K)
Při dosažení meze kluzu se porušuje soudržnost mezi ocelí a betonem. Po dosažení meze kluzu se ocel stává plastickou. Deformace se zvětšuje aniž by rostlo napětí. U ocelí s nevýraznou mezí kluzu, bereme napětí, při kterém je hodnota přetvoření 0,2%.
4.) Mez pevnosti (P)
Po dosažení meze pevnosti se přetvoření prutu dále zvětšuje, i když napětí v prutu klesá. Přetvoření se zvětšuje až do meze destrukce.
5.) Mez destrukce (D)
Při dosažení této meze se prut přetrhne, poměrné přetvoření v okamžiku destrukce je tažnost oceli (okolo 14%).
Klíčová slova:
beton
diagram
napjatost
mezní stavy
železobeton
interakčni diagram
Obsah:
- 1. Pracovní diagram betonu
2. Pracovní diagram oceli
3. Napjatostní stádia v betonu
4. Způsoby porušení prvků z prostého betonu, tvar poměrného přetvoření průřezu, rozdělí napětí po průřezu a průběhy vnitřních sil.
5. Napjatostní stádia v betonu (vyztužený beton)
6. Způsoby porušení prvků z železobetonu, tvar poměrného přetvoření průřezu, rozdělí napětí po průřezu a průběhy vnitřních sil.
7. Koncové úpravy betonářských výztuží, stanovení velikosti kotevní délky, na čem závisí velikost kotevní délky.
8. Rozdělení mezních stavů, jaké znáte mezní stavy, vysvětlete princip metodiky mezních stavů.
9. Základní předpoklady výpočtu podle mezního stavu únosnosti.
10. Z rovnováhy vnitřních sil v odvoďte podmínky rovnováhy (momentovou a součtovou).
11. Nakreslete průběh přetvoření napětí a vnitřní síly pro jednostranně vyztužený průřez.
12. Nakreslete rozdělení přetvoření, napětí a velikosti vnitřních sil pro průřez tvaru „T“, když neutrálná osa prochází žebrem a když prochází deskou.
13. Napište součtovou a momentovou podmínku rovnováhy pro průřez tvaru „T“pokud neutrálná osa prochází žebrem, resp. deskou.
14. Nakreslete rozdělení přetvoření, napětí a vnitřní síly pro oboustranně vyztužený obdélníkový průřez.
15. Napište součtovou a momentovou podmínku rovnováhy pro oboustranně vyztužený obdélníkový průřez.
16. Vysvětlete na prostém nosníku chování železobetonového trámu,tj. nakreslete průběhy napětí tangenciálních a normálových.
17. Vysvětlete princip chování železobetonového prvku při návrhu smykové výztuže, tzv. příhradovou analogii.
18. Popište postup návrhu smykové výztuže zjednodušenou (standardní) metodou, tj. stanovte únosnost tlakové a tahové diagonály.
19. Nakreslete model pro vyjádření výminek rovnováhy v šikmém řezu.
20. Nakreslete model železobetonového nosníku pro odvození únosnosti třmínků.
21. Nakreslete výkres rozdělení materiálu pro jeden prut při spodním povrchu
22. Nakreslete průběhy napětí v průřezu z prostého betonu od zatížení
23. Nakreslete způsoby porušení železobetonových prvků od zatížení
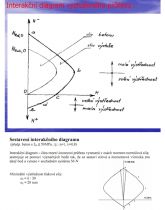
24. Vysvětlete pojem interakční diagram.
25. Nakreslete průběh přetvoření, napětí a vnitřní síly pro rozhodující body interakčního diagramu (v tlačené oblasti).
26. Nakreslete průběh přetvoření, napětí a vnitřní síly pro rozhodující body interakčního diagramu (v tažené oblasti).
27. Napište podmínky rovnováhy pro bod interakčního diagramu ležící na ose, kde se vynáší normálová síla (tlaková), nakreslete přetvoření a vnitřní síly v průřezu.
28. Napište podmínky rovnováhy pro bod interakčního diagramu na rozhraní mezi malou a velkou výstředností v tlaku, nakreslete přetvoření a vnitřní síly v průřezu.
29. Napište podmínky rovnováhy pro bod interakčního diagramu ležící na ose, kde se vynáší ohybový moment, nakreslete přetvoření a vnitřní síly v průřezu.
30. Napište podmínky rovnováhy pro bod interakčního diagramu na rozhraní mezi malou a velkou výstředností v tahu, nakreslete přetvoření a vnitřní síly v průřezu.
31. Napište podmínky rovnováhy pro bod interakčního diagramu ležící na ose, kde se vynáší normálová síla (tahová), nakreslete přetvoření a vnitřní síly v průřezu.
32. Vysvětlete pojem štíhlost, jaký má vliv na únosnost prvku namáhaného kombinací normálové síly a momentu.
33. Vysvětlete pojem účinné délky prutu
34. Jakým způsobem se do výpočtu únosnosti sloupu namáhaného normálovou silou a ohybovým momentem zavádí účinek II. Řádu
35. Jak se projeví ztužení rámové konstrukce na průběhu momentů od účinků II. řádu, (rámy ztužené stěnou, měkká neztužené sloupy).
36. Na čem závisí charakteristická pevnost zdiva
37. Jak se stanový únosnost zdi a na čem závisí.
38. Nakreslete schéma chování stěny do které jsou uloženy dřevěné trámy, jaké zatížení působí na stěnu.
41. Jaké znáte mezní stavy použitelnosti:
42. Vysvětlete pojem ideální průřez, jak se stanový průřezová charakteristika pro ideální průřez.
43. Nakreslete průběh přetvoření a vnitřních sil pro ŽB průřez s trhlinou, napište součtovou a momentovou podmínku rovnováhy.
44. Jak se stanoví moment na mezi vzniku trhlin u ŽB průřezu, na čem závisí jeho hodnota.
45. Na čem závisí šířka trhliny u ŽB průřezu.
46. Vysvětlete pojem ohybová štíhlost a na čem závisí.
47. Na čem závisí deformace prvku.